OR 学会参加！物流と通信を台形で科学する。

前回に引き続き、OR 学会の発表での面白かったものです。

今回の発表は、『台形グラフ構造を有するネットワークにおける迂回度最大要接点を効率的に求めるアルゴリズムの開発 / 本間 宏利さん』です。

この問題の最も重要な点を説明します。例えば電話回線やインターネット回線のノードとエッジがあるじゃないですか。仮に、何かの事故や災害で、ノードの一部が壊れてしまうと、通信を問題なく行う際には、そのノードを迂回して、別のノードを経由して、遠回りをして通信しなくてはなりません。

このように、『もしノード N が壊れた時に、N を迂回した結果、遠回りとなってしまう』という条件を満たすような N を全て求めたいというのがこの発表の問題でした。また、この発表では、このような N のことを要接点と呼んでいます。

この問題は深刻な問題で、ネットワーク内で要接点に対応する端末が故障すると、一対以上の端末間通信のホップ数が増加するため， ネットワーク全体の通信効率が低下してしまいます。

そこで、この『要接点問題』を解くことにより、重要な端末を特定することができ、より安定した通信ネットワークシステムの構築に役立てることが期待できます。

さて、ここで、要接点 N のうち、N が壊れた場合、最も迂回のステップが増加するような N を求める問題を考えます。このような問題を『迂回度最大要接点問題』と言います。

この発表では、迂回度最大要接点問題をいかに効率的なアルゴリズムによって解くか、という問題を扱っていました。

そこでこの発表での結論を言うと、『迂回度最大要接点問題は O(n^2) 時間で解ける！』ということです。(従来までは O(n^3) 時間でした。)

そこで、この発表の一番の目玉。迂回度最大要接点問題を解く際に、台形がどんな役割をするのか？という点です。

以下に、図 を二つ紹介します。

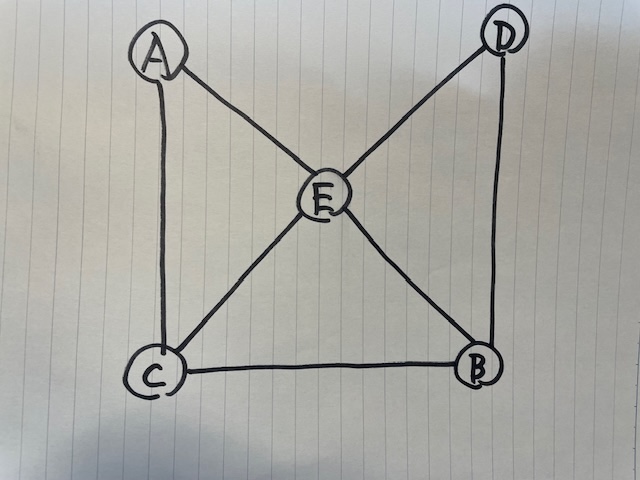
　　　　　　　　　　　　　　　(図 1: 台形グラフ)

　　　　　　　　　　　　　　(図2: 台形モデル)

図 1 の台形グラフは、通常のノードとエッジからなるグラフです。図 2 の台形モデルは、図 1 と次のように対応します。図 2 の台形 A, B, C, D, E は 図 1 のノード A, B, C, D, E に対応します。図 2 の台形 A と C が交差している部分は、図 1 のノード A と C を結ぶエッジに相当します。図 2 の他の台形の交差している部分についても同様です。

ここで、図 1 で、ノード E は要接点となります。なぜならば、E が機能しているときは、A から D への経路は A → E → D と 2 step になりますが、E が壊れてしまうと、A → C → B → D と、ステップがひとつ増えてしまいます。そして、この場合の E の迂回度は（ステップが 1 増えるので）1 と定義します。

それでは、この例がもっと複雑になった場合、つまり迂回度が最大になる要接点をどれだけ効率的なアルゴリズムで求められるか？という問題が発生します。

この発表によると、この問題は、図 1 のノードとエッジを 図 2 の台形の重なり具合で表現しているので、より幾何学的に扱いやすくなります。その結果、迂回度最大要接点問題は、従来知られていた O(n^3) 時間よりももっと速い、O(n^2) 時間で解けるようになりました。

なお、このアルゴリズムの応用で恐ろしいものがあります。それは軍事ですね。軍事拠点をノード、通信や物流の経路をエッジと考えることにより、ある軍事拠点が破壊されても、別の軍事拠点を迂回することにより、効率的な作戦展開が維持できる、というものです。このことは、この発表の後の質疑応答の時間でも指摘されたことです。

最後に、私の疑問を紹介します。それは、アルゴリズムの所要時間を O(n^2) から O(n log n) にまですることができるか？と言う点です。しかしこれは、台形モデルの前身である別のモデルにおいて、すでに O(n^2) での計算量が必要とのことで、その別のモデルの時点で O(n log n) が実現できれば、台形モデルでも O(n log n) が実現できる目処が立つのではないかということです。